Dielectric Properties of NkN
The major drawback of current lead-free piezoelectrics is that their piezoelectric performance is still far lower
than that of the dominating PZT family. Most of the efforts to achieve the piezoelectric properties close to
those of PZT are made in perovskite ferroelectrics. Among these materials, sodium potassium niobate,
Na0.5K0.5NbO3 is a good candidate to replace PZT family because of its high
Curie temperature and good piezoelectric properties.
Another phase diagram of the KNbO3-NaNbO3 system is given in the figure below [1].
There are three morphotropic phase boundaries observed in the phase diagram, located at around 52.5 mol%, 67.5 mol%
and 82.5 mol% NaNbO3 (marked by the dash lines), separating two different orthorhombic phases, respectively.
Around the MPB at 50 mol% NaNbO3 (Na0.5K0.5NbO3) a maximum piezoelectric
performance (d33=80 pC/N, kp=0.36) was found in 1959 [2].
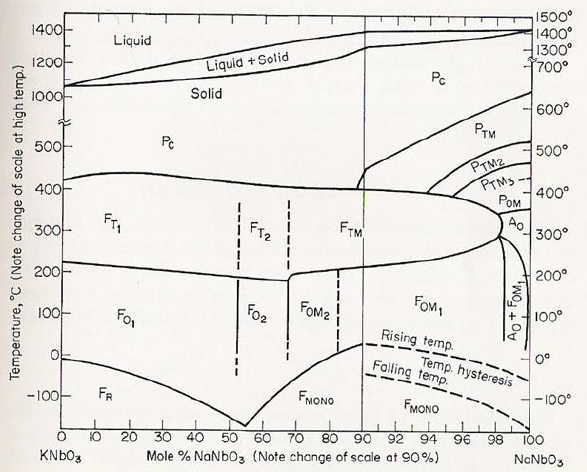
Phase diagram of NabO3 –KNbO3 solid solution [1]
(For comparison see here the phase diagram of PZT.)
NKN shows interesting properties, e.g. a number of ferroelectric
phases with high spontaneous polarization, low dielectric constant, high electromechanical coupling coefficients,
etc [2 - 9]. The constituents of this system are sodium niobate (NaNbO3) and
potassium niobate (KNbO3). NaNbO3 shows structural phase transitions at – 100°C (rhombohedral to orthorhombic)
[10, 11], at 360°C (orthorhombic to orthorhombic), at
480°C (orthorhombic to orthorhombic), at 520°C (orthorhombic to orthorhombic), at 575°C (orthorhombic to
tetragonal) [12], and at 640°C (tetragonal to cubic) [13]. KNbO3 shows structural
phase transitions at – 10°C (rhombohedral to orthorhombic), at 225°C (orthorhombic to tetragonal), and at
420°C (tetragonal to cubic) [14]. At room temperature, NaNbO3, KNbO3 and their
mixtures basically show orthorhombic structure with a small perovskite subcell with monoclinic symmetry [3, 4, 15].
NaNbO3 is antiferroelectric over a wide temperature range but below
– 100°C (rhombohedral structure) it shows ferroelectric behaviour [13]. Doping of small amount
(< 2%) of K at Na site in NaNbO3 makes it ferroelectric below around 400°C and its orthorhombic to
orthorhombic transition temperature shifts towards the orthorhombic to tetragonal transition temperature of
KNbO3 [16]. When doped with 10–100% (mole) K, NaNbO3 shows well-defined ferroelectric
hysteresis loops between room temperature and 400°C. It also shows two transitions, orthorhombic to tetragonal
at 200°C and tetragonal to cubic at 400°C [5]. Above 400°C it becomes paraelectric. Investigators have studied
the temperature variations of dielectric properties of NaNbO3 and KNbO3 single crystals
[4, 5, 17] and polycrystalline Na1–xKxNbO3 [2, 7 - 9].
However, these studies were restricted to low range single frequencies.
Let us observe the variation of the dielectric constant and the loss tangent under variable frequencies, temperatures
and compostions:
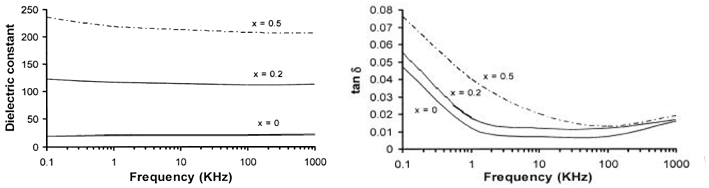
Frequency dependence of dielectric constant and loss tangent in
Na1–xKxNbO3 for different x-values at room temperature.
Frequency dependence of the dielectric constant (left) and the dielectric loss (right) at
room temperature for different x-values in Na1–xKxNbO3 samples are shown in
the figure above.
The dielectric constant and loss tangent, generally, decrease with increasing frequency.
The dielectric constant and loss tangent were observed increasing with increasing x in
Na1–xKxNbO3.
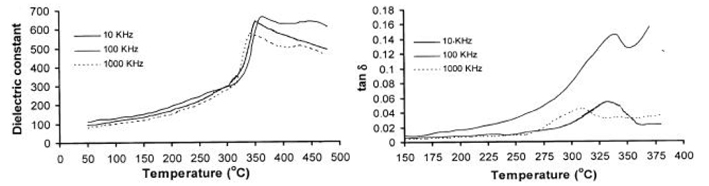
Temperature dependence of dielectric constant and loss tangent at different frequencies in NaNbO3
The observed variation of the dielectric constant with temperature is shown in the next figure for NaNbO3
samples. It was observed that the dielectric constant increases with increasing temperature showing anomaly at
the transition temperature. The peak height at the transition temperature was observed to decrease with increasing
frequency and the dielectric constant peak shifted to lower temperature with increasing frequency, which indicated
the relaxational behaviour of the material [18].
A transition anomaly can be observed at 360°C with a dielectric constant peak value of 661 for 10 KHz; at
350°C with a peak value of 635 for 100 KHz; and at 340°C with a peak value of 570 for 1 MHz.
This anomaly is corresponding to a phase change, from orthorhombic to tetragonal structure [2],
and may be associated to the softening of a vibrational mode, the so-called the soft mode [19 - 23].
Variation of the loss tangent with temperature, is shown on the right side. The dielectric loss is increasing with
increasing temperature and decreasing with increasing frequency. The loss tangent peaks were observed at 340°C
(peak value 0.14) for 10 KHz, at 330°C (peak value 0.05) for 100 KHz, and at 310°C (peak value 0.04) for 1 MHz.
The loss tangent peak shifts to lower temperature with decreasing height and increasing
frequency, showing the relaxational behaviour.
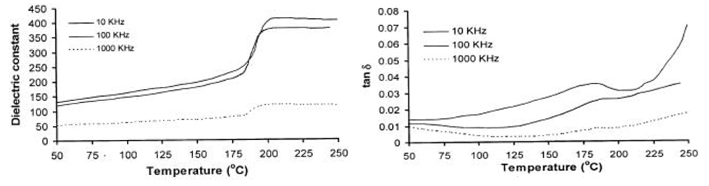
Temperature dependence of dielectric constant and loss tangent at different frequencies in Na80K20NbO3
The figure above shows on the left side the observed temperature dependence
of the dielectric constant for Na80K20NbO3 at different frequencies.
In this composition the dielectric constant also decreases with increasing frequency.The dielectric constant
increases with temperature showing the anomaly at transition temperature.
The peak height decreases and shifts to lower temperature with increasing frequency. The dielectric peaks
were observed at 215°C (peak value 411) for 10 KHz, at 210°C (peak value 380) for 100 KHz, and at 205°C
(peak value 118) for 1 MHz. At the transition temperature the dielectric constant value increases sharply
and remains almost constant thereafter with respect to the temperature variation.
The variation of the loss tangent with temperature is shown on the left side. The loss tangent decreases with
increasing frequency and increases with increasing temperature showing no significant anomaly near the transition
temperature as observed from the dielectric constant measurements.
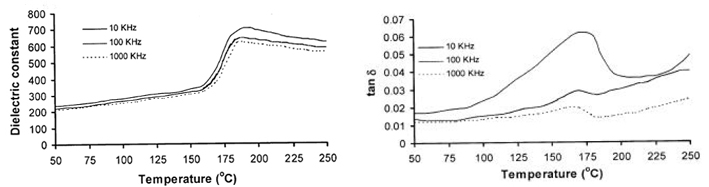
Temperature dependence of dielectric constant and loss tangent at different frequencies in Na50K50NbO3
Finally the temperature dependence of the dielectric constant for the x = 0.5 composition is shown in the last figure.
This composition also shows relaxational behaviour. The dielectric constant peaks were observed at 195°C (peak value
704) for 10 KHz, at 190°C (peak value 650) for 100 KHz, and at 185°C (peak value 617) for 1 MHz.
Beyond the transition temperature the dielectric constant value decreases slightly with increasing temperature.
As before the variation of the loss tangent with temperature for the same composition s shown on the rhkt side.
The loss tangent peaks for 10 KHz, 100 KHz and 1 MHz can be observed at 170°C with peak values 0.06, 0.03
and 0.02, respectively.
Discussion
The dielectric constant and the loss tangent peak heights decrease with increasing frequency
in all the prepared samples. Lossy dielectrics can be represented by the circuit analog
of a resistance in parallel with a capacitor [18]. At higher frequency the capacitor offers low
reactance to the sinusoidal signal, which minimizes the conduction losses in the resistor.
Hence, the value of the dielectric loss decreases at higher frequencies. The present observations are in good
agreement with earlier reported results [2, 4 - 9].
With increasing frequency the dielectric constant peaks were observed shifting to lower temperature in the
present samples. However, for most of the relaxator ferroelectrics the peak of the dielectric constant shifts
to higher temperature with increasing frequency, which has been attributed tom the decreasing relaxation time
with increasing temperature [18]. For Na1–xKxNbO3 system the
relaxation time seems increasing with temperature, and the observed shifting of the dielectric constant peak
to lower temperature with increasing frequency can be due to the increasing relaxation time with temperature
[24].
The damping out of successive relaxation modes is attributed to the decreasing of peak height with frequency
[18]. The anomalous behaviour at certain temperature is due to structural change or phase transition
of the material at that temperature [20, 25 - 30]. The phase transition in the perovskite type materials is,
generally, assumed to be due to the instability of temperature dependent low frequency optical phonon—the soft
phonon mode—at transition temperature. At the transition temperature, frequency of the soft mode tends to be
zero and the lattice displacement associated with it becomes unstable. This explains the observed behaviour of
dielectric properties near the transition temperature.
References:
- B. Jaffe, W. R. Cook, and H. Jaffe, Piezoelectric Ceramics (Academic Press Limited, London, 1971).
- L. Egerton and D. M. Dillon, Journal of the American Ceramic Society 42, 438-442 (1959).
- Wood E A 1951 Acta Crystallogr. 4 353.
- G. Shirane, R. Newnham, and R. Pepinsky, "Dielectric properties and phase transitions of NaNbO3 and
(Na,K)NbO3," Physical Review, 96[3] 581-8 (1954).
- Cross L E 1958 Nature 181 178
- Jaeger R E and Egerton L 1962 J. Am. Ceram. Soc. 45 209
- Heartling G H 1967 J. Am. Ceram. Soc. 50 429
- Narayana Murty S, Umakantham K and Bhanumathi A 1988 Ferroelectrics 82 141
- Narayana Murty S, Rama Murty K V, Umakantham K and Bhanumathi A 1990 Ferroelectrics 102 243
- Wells M and Megaw H D 1961 Proc. Phys. Soc. London 78 1258
- Darlington C N W and Megaw H D 1973 Acta Crystallogr. B29 2171
- Sakowski-Cowley A C, Lukaszewicz K and Megaw H D 1969 Acta Crystallogr. B25 851
- Megaw H D 1974 Ferroelectrics 7 87
- Hellwege K H and Hellwege A M (eds) 1981 Landolt – Bornstein numerical data and functional relationships
in science and technology (New York: Springer Verlag) 16 p. 45
- Tennery V J 1965 J. Am. Ceram. Soc. 48 537
- Ahtee M and Hewat A W 1975 Acta Crystallogr. A31 846
- Matthias B T and Remeika J 1951 Phys. Rev. 82 727
- Goodman G, Buchanan R C and Reynolds III T G 1991 Ceramic
materials for electronics; Processing, properties, and applications
(ed.) R C Buchanan (New York: Marcel Dekker Inc.)
p. 32
- Cochran W 1959 Phys. Rev. Lett. 3 412
- Cochran W 1960 Adv. Phys. 9 387
- Anderson P W 1960 Proc. of conf. on physics of dielectrics
(ed.) G I Skanavi (Moscow: Academy of Sciences) p. 290
- Panwar N S, Upadhyay T C and Semwal B S 1989 Pramana –
J. Phys. 33 603
- Semwal B S and Panwar N S 1992 Bull. Mater. Sci. 15 237
- Lingwal V 2002 Dielectric properties of Na1–xKx(Nb,Ta)O3 systems,
Thesis, H N B Garhwal University, Srinagar (Garhwal)
- Cowley R A 1962 Phys. Rev. Lett. 9 159
- Cowley R A 1964 Phys. Rev. A134 981
- Cowley R A 1965 Philos. Mag. 11 673
- Pytte E and Feder J 1969 Phys. Rev. 187 1077
- Feder J and Pytte E 1970 Phys. Rev. B1 4803
- Pytte E 1972 Phys. Rev. B5 3758







