Diferenças entre edições de "Valores próprios da transformação de um quadrado"
| (Há 15 revisões intermédias de 2 utilizadores que não estão a ser apresentadas) | |||
| Linha 7: | Linha 7: | ||
*ANO: 1 | *ANO: 1 | ||
*LINGUA: pt | *LINGUA: pt | ||
| − | *AUTOR: | + | *AUTOR: Ana Moura Santos e Miguel Dziergwa |
| − | *MATERIA PRINCIPAL: | + | *MATERIA PRINCIPAL: Valores e vetores próprios |
| − | *DESCRICAO: | + | *DESCRICAO: valores próprios da transformação de um quadrado |
| − | *DIFICULDADE: | + | *DIFICULDADE: ** |
| − | *TEMPO MEDIO DE RESOLUCAO: | + | *TEMPO MEDIO DE RESOLUCAO: 15 mn |
| − | *TEMPO MAXIMO DE RESOLUCAO: | + | *TEMPO MAXIMO DE RESOLUCAO: 25 mn |
| − | *PALAVRAS CHAVE: | + | *PALAVRAS CHAVE: transformação linear, matriz que representa a transformação linear, valores próprios reais |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
| − | + | Considere o seguinte quadrado de lados unitários \(Q= \{x \overrightarrow{e_1} + y \overrightarrow{e_2}: x,y \in [0,1] \}\). | |
| − | [[File: | + | [[File:Quad1.gif]] |
| − | + | Indique os valores próprios da transformação linear sofrida pelo quadrado Q, tendo em consideração que o seu transformado se apresenta na figura seguinte, onde cada triângulo é levado no correspondente triângulo da mesma côr. | |
| − | + | [[File:Tr2.gif]] | |
| − | |||
| − | |||
| − | Para obter o zip que contém as instâncias deste exercício clique aqui | + | A) \(\lambda_1 =\)\(2(2+\sqrt{3})\) e \(\lambda_2 =\)\(2(2-\sqrt{3})\); |
| + | |||
| + | B) \(\lambda_1 =\)\(-2(2+\sqrt{3})\) e \(\lambda_2 =\)\(-2(2-\sqrt{3})\); | ||
| + | |||
| + | C) \(\lambda_1 =\)\(4\sqrt{3}\) e \(\lambda_2 =\)\(4-2\sqrt{3}\); | ||
| + | |||
| + | D) \(\lambda_1 =\)\(2(2+\sqrt{3})\) e \(\lambda_2 =\)\(8\). | ||
| + | |||
| + | |||
| + | Para obter o zip que contém as instâncias deste exercício clique aqui[https://drive.tecnico.ulisboa.pt/api/drive/file/1132973717991911/download] | ||
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | ||
Edição atual desde as 17h31min de 5 de outubro de 2017
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Álgebra Linear
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Valores e vetores próprios
- DESCRICAO: valores próprios da transformação de um quadrado
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 25 mn
- PALAVRAS CHAVE: transformação linear, matriz que representa a transformação linear, valores próprios reais
Considere o seguinte quadrado de lados unitários \(Q= \{x \overrightarrow{e_1} + y \overrightarrow{e_2}: x,y \in [0,1] \}\).
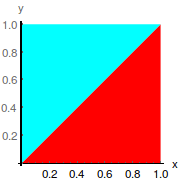
Indique os valores próprios da transformação linear sofrida pelo quadrado Q, tendo em consideração que o seu transformado se apresenta na figura seguinte, onde cada triângulo é levado no correspondente triângulo da mesma côr.
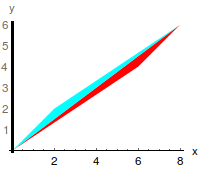
A) \(\lambda_1 =\)\(2(2+\sqrt{3})\) e \(\lambda_2 =\)\(2(2-\sqrt{3})\);
B) \(\lambda_1 =\)\(-2(2+\sqrt{3})\) e \(\lambda_2 =\)\(-2(2-\sqrt{3})\);
C) \(\lambda_1 =\)\(4\sqrt{3}\) e \(\lambda_2 =\)\(4-2\sqrt{3}\);
D) \(\lambda_1 =\)\(2(2+\sqrt{3})\) e \(\lambda_2 =\)\(8\).
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt