Diferenças entre edições de "Valores próprios da transformação de um quadrado"
| Linha 29: | Linha 29: | ||
| − | A1)\(\ | + | A1)\(\lambda_1 =\)\(5+2\sqrt{6}\) e \(\text{SubscriptBox}[\lambda,2]\) |
Para obter o zip que contém as instâncias deste exercício clique aqui(eigenvalqua) | Para obter o zip que contém as instâncias deste exercício clique aqui(eigenvalqua) | ||
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | ||
Revisão das 10h36min de 24 de agosto de 2016
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Álgebra Linear
- ANO: 1
- LINGUA: pt
- AUTOR: Pedro Duarte
- MATERIA PRINCIPAL:
- DESCRICAO:
- DIFICULDADE: easy
- TEMPO MEDIO DE RESOLUCAO: 10 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE:
Considere o seguinte quadrado de lados unitários \(Q= \{x \overrightarrow{e_1} + y \overrightarrow{e_2}: x,y \in [0,1] \}\).
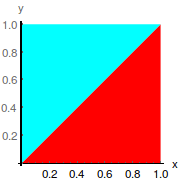
Indique os valores próprios da transformação linear sofrida pelo quadrado Q,tendo em consideração que cada triângulo é levado no correspondente triângulo da mesma côr,e cuja imagem se apresenta de seguida:
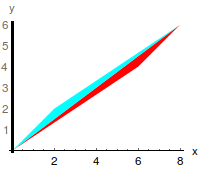
A)\(\left(\begin{array}{c}2\left(2+\sqrt{3}\right)\\2\left(2-\sqrt{3}\right)\\\end{array}\right)\), B)\(\left(\begin{array}{c}-2\left(2+\sqrt{3}\right)\\-2\left(2-\sqrt{3}\right)\\\end{array}\right)\), C)\(\left(\begin{array}{c}4\sqrt{3}\\4-2\sqrt{3}\\\end{array}\right)\), D)\(\left(\begin{array}{c}2\left(2+\sqrt{3}\right)\\8\\\end{array}\right)\)
A1)\(\lambda_1 =\)\(5+2\sqrt{6}\) e \(\text{SubscriptBox}[\lambda,2]\)
Para obter o zip que contém as instâncias deste exercício clique aqui(eigenvalqua)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt