Superfície paramétrica
Saltar para a navegação
Saltar para a pesquisa
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo diferencial e integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Funções de \(R^n\) em \(R^m\): limite e continuidade
- DESCRICAO: Superfície paramétrica
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE: parametrização de uma superfície, função parametrização
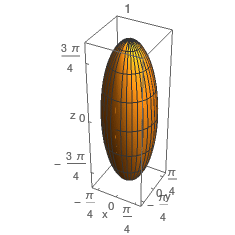
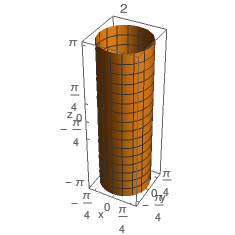
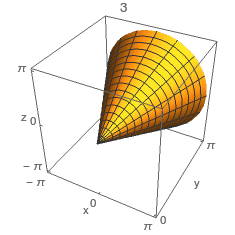
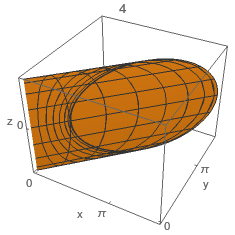
Seja \(F\) a função vetorial \(\text{F:D$\subset$}\mathbb{R}^2\text{$\to$}\mathbb{R}^3\),\(F\)\(\left(\begin{array}{c}u\\v\\\end{array}\right)\)=\(\left(\begin{array}{c}\cos(u)\\\sin(u)\\v\\\end{array}\right)\) onde \(\text{D=[}-2\pi\text{,}0\text{]$\times$[}-\pi\text{,}\pi\text{]}\), que define uma parametrização de uma dada superfície \(S\). Considere as 4 figuras abaixo.
Qual poderá corresponder á parametrização da superfície \(S\)?
A) \(1\)
B) \(2\)
C) \(3\)
D) \(4\)
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt