Somas de Darboux 0-5n
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo diferencial e integral 1
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL:
- DESCRICAO:
- DIFICULDADE: *
- TEMPO MEDIO DE RESOLUCAO: 10 mn
- TEMPO MAXIMO DE RESOLUCAO: 15 mn
- PALAVRAS CHAVE:
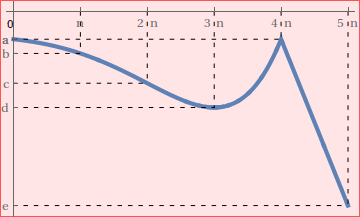
Na figura abaixo está representado o gráfico da função \(f\) e a decomposição \(\text{$\{$0,n,2n,3n,4n,5n$\}$}\) do intervalo \(\text{[0,5n],n$\in$$\mathbb{N}$}\).
A) A soma inferior de Darboux da função \(\text{f}\), para a decomposição indicada é \(\text{n}(\text{b}+\text{c}+2\text{d}+\text{e})\),
B) \(\int_0^{5n}\text{f}(x)\,dx\leq\text{n}(\text{b}+\text{c}+2\text{d}+\text{e})\),
C) A soma superior de Darboux da função \(\text{f}\), para a decomposição indicada é \(\text{n}(4\text{a}+\text{b}+\text{c})\),
D) A soma inferior de Darboux da função \(\text{f}\), para a decomposição indicada é \(\text{n}(3\text{a}+\text{b}+\text{c})\)
Para obter o zip que contém as instâncias deste exercício clique aqui(somas)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt