Diferenças entre edições de "Radiare"
(Texto inicial) |
(Imagens.) |
||
| Linha 1: | Linha 1: | ||
| − | =Introdução teórica= | + | '''Navegação:''' [[Página principal|Mysolutions]] > [[MOOC FEX]] > Radiare |
| + | |||
| + | ==Introdução teórica== | ||
Nesta experiência vamos debruçar-nos sobre um conceito bastante comum na natureza, os eventos aleatórios, e vamos estudar uma das ferramentas mais comuns para estudar estes fenómenos: o histograma. | Nesta experiência vamos debruçar-nos sobre um conceito bastante comum na natureza, os eventos aleatórios, e vamos estudar uma das ferramentas mais comuns para estudar estes fenómenos: o histograma. | ||
A definição de evento aleatório cai fora do âmbito deste curso, mas no dia a dia temos vários exemplos: os números da lotaria, EXEMPLO, EXEMPLO, EXEMPLO... | A definição de evento aleatório cai fora do âmbito deste curso, mas no dia a dia temos vários exemplos: os números da lotaria, EXEMPLO, EXEMPLO, EXEMPLO... | ||
| − | Um dos primeiros eventos aleatórios com que um estudante de física é confrontado é o decaimento radioactivo. Mas | + | Um dos primeiros eventos aleatórios com que um estudante de física é confrontado é o decaimento radioactivo. Mas antes, uma pequena experiência para fazer em casa. |
| − | =A experiência em casa= | + | ==A experiência em casa== |
Em casa, sugerimos uma experiência simples de lançar X dados múltiplas vezes. O tipo mais comum de dados é o D6 (mostrar foto), mas esta experiência pode ser feita com qualquer tipo (mostrar imagens de outros tipos de dados). Em cada lançamento registamos o valor da soma das faces. Ao lançar 18 vezes, ficamos com esta lista de valores: | Em casa, sugerimos uma experiência simples de lançar X dados múltiplas vezes. O tipo mais comum de dados é o D6 (mostrar foto), mas esta experiência pode ser feita com qualquer tipo (mostrar imagens de outros tipos de dados). Em cada lançamento registamos o valor da soma das faces. Ao lançar 18 vezes, ficamos com esta lista de valores: | ||
| Linha 14: | Linha 16: | ||
Ao apresentarmos os dados desta forma não dizem nada. É aqui que entra o histograma. Em vez de simplesmente escre-ver o valor, vamos representa-lo graficamente. | Ao apresentarmos os dados desta forma não dizem nada. É aqui que entra o histograma. Em vez de simplesmente escre-ver o valor, vamos representa-lo graficamente. | ||
| − | ( | + | (Video da construção do histograma.) |
| + | |||
| + | Em vez disso, vamos construir um gráfico. No eixo horizontal temos os valores possíveis. No vertical, o nº de vezes que observamos esse valor. Cada vez que aparece, colorimos uma quadricula. | ||
| − | Fazemos agora uma 2ª experiência, desta vez com mais lançamentos, 36: (gráfico já feito ou time lapse do lançar os | + | Fazemos agora uma 2ª experiência, desta vez com mais lançamentos, 36: (gráfico já feito ou time lapse do lançar os dados / desenhar) |
Uma 3ª, agora com 48: | Uma 3ª, agora com 48: | ||
| Linha 22: | Linha 26: | ||
Como podemos ver, a distribuição dos resultados aproxima-se cada vez mais de uma curva normal (também conhecida como Gaussiana). Quanto mais lançamentos forem registados, mais próximo o histograma fica da curva. É isto que signi-fica limite da distribuição, mais isso fica fora do âmbito deste curso. | Como podemos ver, a distribuição dos resultados aproxima-se cada vez mais de uma curva normal (também conhecida como Gaussiana). Quanto mais lançamentos forem registados, mais próximo o histograma fica da curva. É isto que signi-fica limite da distribuição, mais isso fica fora do âmbito deste curso. | ||
| − | PERGUNTAS: média da distribuição? Desvio padrão? Porque somamos vários dados em vez de lançar apenas um e | + | PERGUNTAS: média da distribuição? Desvio padrão? Porque somamos vários dados em vez de lançar apenas um e registar a face? |
| − | =A experiência no e-lab= | + | ==A experiência no e-lab== |
Chega agora o momento de estudar o decaimento radioactivo, que já foi aludido. Este fenómeno é aleatório porque não há nenhuma lei que defina quando é que um determinado núcleo irá decair. Apenas conseguimos aproximar quantos nú-cleos decaem num determinado intervalo de tempo, se conhecermos algumas informações sobre a amostra e o elemento em causa. | Chega agora o momento de estudar o decaimento radioactivo, que já foi aludido. Este fenómeno é aleatório porque não há nenhuma lei que defina quando é que um determinado núcleo irá decair. Apenas conseguimos aproximar quantos nú-cleos decaem num determinado intervalo de tempo, se conhecermos algumas informações sobre a amostra e o elemento em causa. | ||
| Linha 35: | Linha 39: | ||
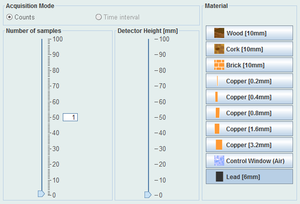
A distância entre a amostra e o material escolhido é sempre a mesma, mas o utilizador pode escolher posicionar o detector a diferentes alturas, mudando a distância amostra / detector. | A distância entre a amostra e o material escolhido é sempre a mesma, mas o utilizador pode escolher posicionar o detector a diferentes alturas, mudando a distância amostra / detector. | ||
| − | + | [[File:RadiareControlo.png|thumb|]] | |
Na sala de controlo temos 3 parâmetros que podemos modificar: | Na sala de controlo temos 3 parâmetros que podemos modificar: | ||
| Linha 42: | Linha 46: | ||
*O material a usar. | *O material a usar. | ||
| − | + | [[File:RadiareOutput.png|thumb|]] | |
| − | |||
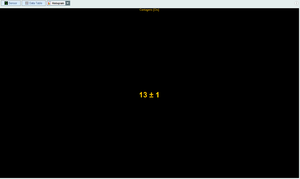
Assim que corremos a experiência, vemos este número. O que é que significa? Este é o número de eventos que o dector “viu” durante 1 segundo. Este número por sí só não nos diz muito: pode ser tentador usa-lo directamente, mas não o de-vemos fazer. Porque o decaimento é um evento aleatório, pode haver mais núcleos a decair num determinado intervalo do que no seguinte. A lei do decaimento dita que a MÉDIA do número de decaimentos tende para um certo valor. Por esta razão o e-lab regista várias amostras em intervalos definidos. | Assim que corremos a experiência, vemos este número. O que é que significa? Este é o número de eventos que o dector “viu” durante 1 segundo. Este número por sí só não nos diz muito: pode ser tentador usa-lo directamente, mas não o de-vemos fazer. Porque o decaimento é um evento aleatório, pode haver mais núcleos a decair num determinado intervalo do que no seguinte. A lei do decaimento dita que a MÉDIA do número de decaimentos tende para um certo valor. Por esta razão o e-lab regista várias amostras em intervalos definidos. | ||
| − | + | Tabela de resultados | |
| − | |||
No final obtemos uma tabela com X linhas, em que X é o número de amostras pedidas. Podemos gravar a tabela o que nos deixa com um ficheiro CSV. Se tiver dificuldades em extrair a informação deste ficheiro, temos um tutorial na página com as configurações necessárias. | No final obtemos uma tabela com X linhas, em que X é o número de amostras pedidas. Podemos gravar a tabela o que nos deixa com um ficheiro CSV. Se tiver dificuldades em extrair a informação deste ficheiro, temos um tutorial na página com as configurações necessárias. | ||
| Linha 53: | Linha 55: | ||
Vamos usar programa Microsoft Excel, mas qualquer programa de folha de cálculo (LibreOffice, OpenOffice, etc) funcio-na de uma maneira semelhante. Selecionamos a coluna com os resultados pretendidos e copiamos para uma nova folha. Este programa tem um menu próprio para inserir um histograma. Selecionamos os valores, escolhemos a opção adequada e voilà. Temos assim um histograma. | Vamos usar programa Microsoft Excel, mas qualquer programa de folha de cálculo (LibreOffice, OpenOffice, etc) funcio-na de uma maneira semelhante. Selecionamos a coluna com os resultados pretendidos e copiamos para uma nova folha. Este programa tem um menu próprio para inserir um histograma. Selecionamos os valores, escolhemos a opção adequada e voilà. Temos assim um histograma. | ||
| − | + | [[File:RadiareExcel.png|thumb|]] | |
Para obtermos a média e o desvio padrão, fazemos MEAN ou MEDIA e STDEV ou DESV, respectivamente. A média da distribuição dá-nos uma ideia mais correcta da actividade da amostra, e é este valor que devemos usar para comparar os vários materiais | Para obtermos a média e o desvio padrão, fazemos MEAN ou MEDIA e STDEV ou DESV, respectivamente. A média da distribuição dá-nos uma ideia mais correcta da actividade da amostra, e é este valor que devemos usar para comparar os vários materiais | ||
Revisão das 00h40min de 1 de janeiro de 2016
Navegação: Mysolutions > MOOC FEX > Radiare
Introdução teórica
Nesta experiência vamos debruçar-nos sobre um conceito bastante comum na natureza, os eventos aleatórios, e vamos estudar uma das ferramentas mais comuns para estudar estes fenómenos: o histograma.
A definição de evento aleatório cai fora do âmbito deste curso, mas no dia a dia temos vários exemplos: os números da lotaria, EXEMPLO, EXEMPLO, EXEMPLO...
Um dos primeiros eventos aleatórios com que um estudante de física é confrontado é o decaimento radioactivo. Mas antes, uma pequena experiência para fazer em casa.
A experiência em casa
Em casa, sugerimos uma experiência simples de lançar X dados múltiplas vezes. O tipo mais comum de dados é o D6 (mostrar foto), mas esta experiência pode ser feita com qualquer tipo (mostrar imagens de outros tipos de dados). Em cada lançamento registamos o valor da soma das faces. Ao lançar 18 vezes, ficamos com esta lista de valores:
(imagem dos números escritos)
Ao apresentarmos os dados desta forma não dizem nada. É aqui que entra o histograma. Em vez de simplesmente escre-ver o valor, vamos representa-lo graficamente.
(Video da construção do histograma.)
Em vez disso, vamos construir um gráfico. No eixo horizontal temos os valores possíveis. No vertical, o nº de vezes que observamos esse valor. Cada vez que aparece, colorimos uma quadricula.
Fazemos agora uma 2ª experiência, desta vez com mais lançamentos, 36: (gráfico já feito ou time lapse do lançar os dados / desenhar)
Uma 3ª, agora com 48:
Como podemos ver, a distribuição dos resultados aproxima-se cada vez mais de uma curva normal (também conhecida como Gaussiana). Quanto mais lançamentos forem registados, mais próximo o histograma fica da curva. É isto que signi-fica limite da distribuição, mais isso fica fora do âmbito deste curso.
PERGUNTAS: média da distribuição? Desvio padrão? Porque somamos vários dados em vez de lançar apenas um e registar a face?
A experiência no e-lab
Chega agora o momento de estudar o decaimento radioactivo, que já foi aludido. Este fenómeno é aleatório porque não há nenhuma lei que defina quando é que um determinado núcleo irá decair. Apenas conseguimos aproximar quantos nú-cleos decaem num determinado intervalo de tempo, se conhecermos algumas informações sobre a amostra e o elemento em causa. Para esta experiência usamos a sala de controlo Radiare. Esta é uma das experiências que mostra a força do e-lab: são raras as escolas básicas ou secundárias que têm acesso a amostras radioactivas.
(vídeo da montagem a mexer-se)
A montagem é composta por um detector de Geiger-Müller posicionado por cima de uma amostra radioactiva de Amerício 95. Entre o detector e a amostra, temos um tapete com várias amostras. Cada uma dessas posições corresponde um mate-rial diferente. A distância entre a amostra e o material escolhido é sempre a mesma, mas o utilizador pode escolher posicionar o detector a diferentes alturas, mudando a distância amostra / detector.
Na sala de controlo temos 3 parâmetros que podemos modificar:
- Altura do detector;
- Número de amostras a registar;
- O material a usar.
Assim que corremos a experiência, vemos este número. O que é que significa? Este é o número de eventos que o dector “viu” durante 1 segundo. Este número por sí só não nos diz muito: pode ser tentador usa-lo directamente, mas não o de-vemos fazer. Porque o decaimento é um evento aleatório, pode haver mais núcleos a decair num determinado intervalo do que no seguinte. A lei do decaimento dita que a MÉDIA do número de decaimentos tende para um certo valor. Por esta razão o e-lab regista várias amostras em intervalos definidos. Tabela de resultados
No final obtemos uma tabela com X linhas, em que X é o número de amostras pedidas. Podemos gravar a tabela o que nos deixa com um ficheiro CSV. Se tiver dificuldades em extrair a informação deste ficheiro, temos um tutorial na página com as configurações necessárias.
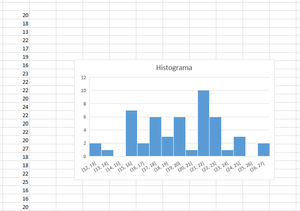
Vamos usar programa Microsoft Excel, mas qualquer programa de folha de cálculo (LibreOffice, OpenOffice, etc) funcio-na de uma maneira semelhante. Selecionamos a coluna com os resultados pretendidos e copiamos para uma nova folha. Este programa tem um menu próprio para inserir um histograma. Selecionamos os valores, escolhemos a opção adequada e voilà. Temos assim um histograma.
Para obtermos a média e o desvio padrão, fazemos MEAN ou MEDIA e STDEV ou DESV, respectivamente. A média da distribuição dá-nos uma ideia mais correcta da actividade da amostra, e é este valor que devemos usar para comparar os vários materiais
Os protocolos sugeridos implicam fazer este processo várias vezes (uma para cada configuração).
PERGUNTAS: Qual é a semi-espessura do cobre?