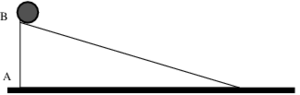
Plano inclinado, Disco vs Anel
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Mecânica e ondas
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Mourão
- MATERIA PRINCIPAL: Momento de Inércia
- DESCRICAO: Plano inclinado, Disco vs Anel
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 1200 [s]
- TEMPO MAXIMO DE RESOLUCAO: 2400 [s]
- PALAVRAS CHAVE: Momento, inércia, rotação, corpo, rígido, plano, inclinado, angular, disco, anél
Um disco e um anel rodam sem deslizar por um plano inclinado, partindo ambos de uma altura \(h\). Considere as massas do anel e do disco iguais e \(m=200\) g, e os raios do anel e do disco iguais a \(r=10\) cm. O plano inclinado faz um ângulo de \(\theta = 15^º\) com a horizontal. Considere \(g = 9.81 \) m s\(^{-2}\)
- Quais as forças que actuam no anel durante o movimento ao longo do plano? E no disco?
Respostas
As forças que actuam no anel são iguais às que actuam no disco, nomeadamente o seu peso, a força de atrito e a reacção normal da superfície.
- Calcule os momentos de inércia do disco e do anel relativamente ao ponto que passa no centro de cada um e é perpendicular ao plano de rotação.
Respostas
- \( I_{anel} = 0.002 \) Kg m\(^2\)
- \( I_{disco} = 0.001 \) Kg m\(^2\)
- Calcule a aceleração do anel e a aceleração do disco durante este movimento.
Respostas
- \( a_{anel} \simeq 1.27 \) m s\(^{-2}\)
- \( a_{disco} \simeq 1.69 \) m s\(^{-2}\)
- Calcule a energia cinética de translação e a energia cinética de rotação do anel e do disco quando se deslocaram 2 metros ao longo do plano inclinado.
Respostas
Para o anel:
- \(E_{c t} \simeq 0.51\) J
- \(E_{c r} \simeq 0.51\) J
Para o disco:
- \(E_{c t} \simeq 0.68\) J
- \(E_{c r} \simeq 0.34\) J
- Qual dos dois (anel ou disco) chega primeiro ao fim do plano inclinado? Justifique.
Respostas
O que chega primeiro é o disco pois, uma vez que tem um momento de inércia mais pequeno, consegue que uma percentagem maior da energia potencial gravítica se transforme em energia cinética de translação.