Pêndulo Mundial
Navegação: Mysolutions > MOOC FEX > Pêndulo Mundial
Introdução teórica
O pêndulo simples é uma das experiências básicas em física.
Quando a massa é afastada da posição de equilíbrio (mantendo o fio direito) e largada, esta descreve um movimento periódico amortecido .
O esquema normalmente usado para representar este sistema físico é apresentado na figura 1.
(falta a imagem)
O equilíbrio de forças a actuar na massa é [math]P \ sen \ \theta = T[/math] onde [math]P = m g[/math] e [math]T = m a[/math]. Substituindo obtemos (para um comprimento fixo)
[math] - m g \ sen \ \theta = m l \frac{d^2 \theta}{d t^2}[/math]
Se considerarmos a aproximação de pequenos ângulos (ou seja, [math]sen \theta \approx \theta[/math]) podemos escrever
[math] \frac{d^2 \theta}{d t^2} + \omega _0 ^2 = 0[/math] onde [math] \omega _0 = \sqrt{ \frac{g}{l} }[/math]
E o periodo do movimento é
[math]T = \frac{\omega}{2 \pi} = 2 \pi \sqrt{ \frac{l}{g} }[/math]
que, como podemos observar, depende apenas do comprimento do fio e da aceleração gravítica.
No programa de física 12º ano (confirmar isto) usa-se esta equação para, dado o comprimento de um pêndulo e uma ace-leração gravítica aproximada, se obter o período.
Nesta actividade experimental vamos fazer o inverso: medir o período de um pêndulo para estudar o valor local da acele-ração gravítica. Mas antes disso, uma pequena experiência para fazer em casa:
A experiência em casa
A construção de um pêndulo em casa é simples. No entanto, ao pensar na montagem, há sempre que ter em mente a re-produtibilidade das medições, ou seja, construir uma montagem que possa ser feita novamente, se necessário no outro lado do mundo. Uma montagem sugerida é:
(foto)
Ingredientes:
- Um yoyo que será o pêndulo;
- Um anteparo para ajudar a ajustar a posição inicial (e, consequentemente, a amplitude do movimento);
- Uma fita métrica na mesa para medir a posição;
- Um cronómetro (ou telemóvel com função de cronómetro);
- Um ponto de fixação.
Com esta montagem simples podemos estudar a forma como a variação da amplitude inicial ou do comprimento do fio afecta o período. (Amplitudes / comprimentos sugeridos?)
Ao medir o tempo para n períodos ininterruptamente (fazendo depois a média) reduzimos o erro experimental do período (fica como desafio perceber porquê). A autora M. C. Abreu sugere 5 medições de 10 períodos. (pág 36, fundo)
A experiência no e-lab
(consideramos apenas as oscilações iniciais, após terem estabilizado, para que o período se mantenha mais ou menos constante)
O projecto Pêndulo Mundial tem como objectivo evidênciar aos estudantes a variação de g com a latitude.
Cada sala de controlo corresponde a uma das várias montagens com as mesmas características físicas, cada uma posicio-nada em pontos diferentes do globo, o que significa que cada sala pode ser usada para fazer o mesmo estudo que foi feito do o pêndulo caseiro numa montagem maior (o pêndulo mundial tem cerca de 3 metros de altura).
A montagem dos pêndulos consiste num peso (usamos um peso de arremesso), um fio (aço?), um ponto de apoio (este sim difere nas montagens, mas é irrelevante) e um sistema de lançamento.
(vídeo do pêndulo a começar)
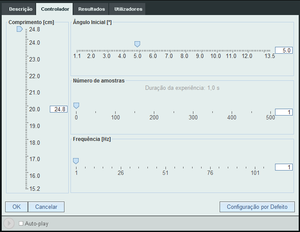
A sala de controlo permite escolher o ângulo inicial, o número de amostras e a frequência de aquisição.
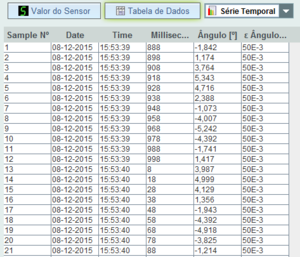
A tabela de resultados obtida tem esta forma:
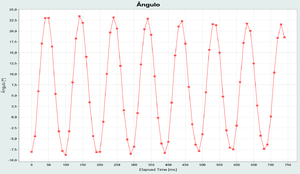
Cada uma das amostras corresponde à posição do pêndulo num determinado instante. A interface do e-lab também mostra um gráfico com os resultados:
Vamos escolher as oscilações iniciais, após terem estabilizado, para que o período se mantenha mais ou menos constante)
Fazemos o registo de alguns períodos e determinamos g a partir da equação já deduzida: [math]g = \frac{4 \pi ^2 L}{T^2}[/math]
Este processo pode ser repetido para vários pontos do globo, e os resultados plotados em função da latitude. Para compa-rar com valores esperados, podemos usar a equação dada pelo World GeodeticSystem Datum Surface:
[math]g_n (\varphi) = 9,780 326 772 \ \left[ 1 + 0.005 302 33 \ sin^2(\varphi) - 0,000 005 89 \ sin^2 \left( \frac{2}{\varphi} \right) \right] [/math]
Últimas considerações
- Definir bem o comprimento do pêndulo (fio + raio da esfera).
- Não esquecer a aproximação de pequenos ângulos, para amplitudes grandes a expressão para o período deixa de ser válida.
- Desprezar as oscilações iniciais (para que os transientes desapareçam).
- Não esquecer que os valores têm um offset causado por especificidades da montagem.
- Pode usar-se um bengaleiro para fixar o pêndulo
- Pode fazer-se a experiência encostada a um espelho ou vidro/janela para reduzir os erros de paralaxe