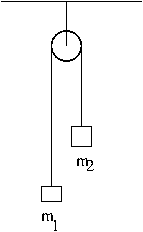
Máquina de Atwood com roldana
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Mecânica e ondas
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Mourão
- MATERIA PRINCIPAL: Momento de Inércia
- DESCRICAO: Máquina de Atwood com roldana
- DIFICULDADE: ***
- TEMPO MEDIO DE RESOLUCAO: 1200 [s]
- TEMPO MAXIMO DE RESOLUCAO: 2400 [s]
- PALAVRAS CHAVE: Máquina, atwood, roldana, momento, inércia, rotação, corpo, rígido
Considere o sistema representado por uma roldana e duas massas. As duas massas \(m_1\) e \(m_2\) estão ligadas entre si por uma corda que passa pela roldana, como se vê na figura ao lado. A roldana pode ser aproximada por um disco de massa \(m_r=600\) g e raio \(R=2\) cm.
Considere o referencial em que a coordenada y das massas aumenta quando estas sobem.
- Quais as expressões para a aceleração com que se deslocam as massas \(m_1\) e \(m_2\)? Compare com o resultado obtido para o caso com inércia da roldana desprezável.
Respostas
\( a_1 = -a_2 = a = - \frac{m_1 - m_2}{m_1 + m_2 + \frac{m_R}{2}} g \)
No caso em que a inércia da roldana era desprezável tinhamos:
\( a_1 = -a_2 = a = - \frac{m_1 - m_2}{m_1 + m_2} g \)
Vemos assim, então, que a diferença está no termo \(\frac{m_R}{2}\), que se deve à inércia da roldana e que tem como efeito diminuir o valor da aceleração.
- Qual a aceleração angular da roldana?
Respostas
\( \alpha = \frac{a}{R} = - \frac{m_1 - m_2}{m_1 + m_2 + \frac{m_R}{2}} \frac{g}{R} \)
- Qual a relação entre as massas para que o sistema esteja em equilíbrio?
Respostas
\( m_1 = m_2 \)
As massas têm que ser iguals, tal como no caso da inércia da roldana desprezável.
- Considere \(m_1 = 200\) g e \(m_2 = 100\) g. Calcule o valor das acelerações \(a_1\) e \(a_2\). Compare com a aceleração da gravidade.
Respostas
\( a_1 = - a_2 = - \frac{1}{6} g \)