Diferenças entre edições de "Identificar função a partir de curvas"
Saltar para a navegação
Saltar para a pesquisa
(Criou a página com "<div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> '''Metadata''' <div class="mw-collapsible-content"> *CONTEXTO : Primeiro ciclo universitário *AREA:...") |
|||
| (Há 2 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 4: | Linha 4: | ||
*CONTEXTO : Primeiro ciclo universitário | *CONTEXTO : Primeiro ciclo universitário | ||
*AREA: Matemática | *AREA: Matemática | ||
| − | *DISCIPLINA: Calculo | + | *DISCIPLINA: Calculo Diferencial e Integral 2 |
*ANO: 1 | *ANO: 1 | ||
*LINGUA: pt | *LINGUA: pt | ||
| − | *AUTOR: | + | *AUTOR: Ana Moura Santos e Miguel Dziergwa |
| − | *MATERIA PRINCIPAL: | + | *MATERIA PRINCIPAL: Funções de \(R^n\) em \(R^m\): limite e continuidade |
| − | *DESCRICAO: | + | *DESCRICAO: Identificar a representação algébrica da função a partir de curvas de nível |
| − | *DIFICULDADE: | + | *DIFICULDADE: * |
*TEMPO MEDIO DE RESOLUCAO: 15 mn | *TEMPO MEDIO DE RESOLUCAO: 15 mn | ||
| − | *TEMPO MAXIMO DE RESOLUCAO: | + | *TEMPO MAXIMO DE RESOLUCAO: 20 mn |
| − | *PALAVRAS CHAVE: | + | *PALAVRAS CHAVE: funções de \(R^2\) em \(R\), funções escalares, representação algébrica, curvas de nível |
</div> | </div> | ||
</div> | </div> | ||
| Linha 21: | Linha 21: | ||
Indique a única expressão, entre as seguintes, que corresponde à função f(x,y). | Indique a única expressão, entre as seguintes, que corresponde à função f(x,y). | ||
| − | A)\(\cos\left(\sqrt{-x^2-y^2+9}\right)\) | + | A) \(\cos\left(\sqrt{-x^2-y^2+9}\right)\) |
| − | B)\(e^{\sqrt{-x^2-y^2+9}}\) | + | B) \(e^{\sqrt{-x^2-y^2+9}}\) |
| − | C)\(-x^2-\frac{y^2}{16}+16\) | + | C) \(-x^2-\frac{y^2}{16}+16\) |
| − | D)\(\sin(3x)\) | + | D) \(\sin(3x)\) |
Para obter o zip que contém as instâncias deste exercício clique aqui(curvas2) | Para obter o zip que contém as instâncias deste exercício clique aqui(curvas2) | ||
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt | ||
Edição atual desde as 19h54min de 20 de março de 2018
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo Diferencial e Integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Funções de \(R^n\) em \(R^m\): limite e continuidade
- DESCRICAO: Identificar a representação algébrica da função a partir de curvas de nível
- DIFICULDADE: *
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 20 mn
- PALAVRAS CHAVE: funções de \(R^2\) em \(R\), funções escalares, representação algébrica, curvas de nível
Na figura seguinte podem ver-se curvas de nível de uma determinada função f(x,y) . As zonas claras correspondem a valores mais elevados e as zonas escuras a valores mais baixos da função. A diferença dos valores da função em duas linhas de nível consecutivas é constante.
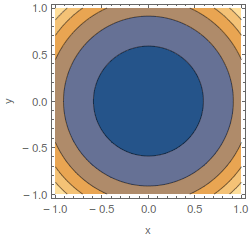Indique a única expressão, entre as seguintes, que corresponde à função f(x,y).
A) \(\cos\left(\sqrt{-x^2-y^2+9}\right)\)
B) \(e^{\sqrt{-x^2-y^2+9}}\)
C) \(-x^2-\frac{y^2}{16}+16\)
D) \(\sin(3x)\)
Para obter o zip que contém as instâncias deste exercício clique aqui(curvas2)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt