Funções trigonométricas
Saltar para a navegação
Saltar para a pesquisa
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Mecânica e ondas
- ANO: 1
- LINGUA: pt
- AUTOR: Nuno Pinhão
- MATERIA PRINCIPAL: Revisões de conceitos de Matemática
- DESCRICAO: Trigonometria
- DIFICULDADE: *
- TEMPO MEDIO DE RESOLUCAO: 30 [s]
- TEMPO MAXIMO DE RESOLUCAO: 60 [s]
- PALAVRAS CHAVE: Seno, coseno
Considere a figura do triângulo e o ângulo \(\alpha\) no vértice em A.
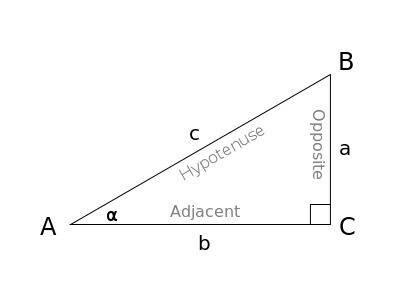
- Indique, em função dos lados do triângulo, quais as definições correctas:
- Cosseno de \(\alpha\):
Respostas
a) \(\cos \alpha = \dfrac{a}{b} \)
b) \(\cos \alpha = \dfrac{b}{c} \)
c) \(\cos \alpha = \dfrac{a}{c} \)
d) \(\cos \alpha = \dfrac{c}{b} \)
e) \(\cos \alpha = \dfrac{b}{a} \)
- Seno de \(\alpha\):
Respostas
a) \(\sin \alpha = \dfrac{a}{b} \)
b) \(\sin \alpha = \dfrac{b}{c} \)
c) \(\sin \alpha = \dfrac{a}{c} \)
d) \(\sin \alpha = \dfrac{c}{b} \)
e) \(\sin \alpha = \dfrac{b}{a} \)
- Tangente de \(\alpha\):
Respostas
a) \(\tan \alpha = \dfrac{a}{b} \)
b) \(\tan \alpha = \dfrac{b}{c} \)
c) \(\tan \alpha = \dfrac{a}{c} \)
d) \(\tan \alpha = \dfrac{c}{b} \)
e) \(\tan \alpha = \dfrac{b}{a} \)