Diferenças entre edições de "Função densidade marginal num ponto"
Saltar para a navegação
Saltar para a pesquisa
| Linha 8: | Linha 8: | ||
*LINGUA: pt | *LINGUA: pt | ||
*AUTOR: Equipa de Probabilidades e Estatística | *AUTOR: Equipa de Probabilidades e Estatística | ||
| − | *MATERIA PRINCIPAL: Distribuições conjuntas e complementos | + | *MATERIA PRINCIPAL: Distribuições conjuntas de probabilidade e complementos |
*DESCRICAO: Probabilidades I | *DESCRICAO: Probabilidades I | ||
*DIFICULDADE: Easy | *DIFICULDADE: Easy | ||
*TEMPO MEDIO DE RESOLUCAO: 10 min | *TEMPO MEDIO DE RESOLUCAO: 10 min | ||
*TEMPO MAXIMO DE RESOLUCAO: 15 min | *TEMPO MAXIMO DE RESOLUCAO: 15 min | ||
| − | *PALAVRAS CHAVE: | + | *PALAVRAS CHAVE: Par aleatório discreto, função de probabilidade conjunta, função de distribuição marginal |
</div> | </div> | ||
</div> | </div> | ||
Revisão das 12h32min de 8 de abril de 2017
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Probabilidades e Estatística
- ANO: 2
- LINGUA: pt
- AUTOR: Equipa de Probabilidades e Estatística
- MATERIA PRINCIPAL: Distribuições conjuntas de probabilidade e complementos
- DESCRICAO: Probabilidades I
- DIFICULDADE: Easy
- TEMPO MEDIO DE RESOLUCAO: 10 min
- TEMPO MAXIMO DE RESOLUCAO: 15 min
- PALAVRAS CHAVE: Par aleatório discreto, função de probabilidade conjunta, função de distribuição marginal
Suponha que as variáveis aleatórias \(X\) e \(Y\) possuem função de probabilidade conjunta dada por: 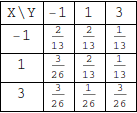 Determine o valor da função de distribuição marginal de \(X\) no ponto \(1\).
Determine o valor da função de distribuição marginal de \(X\) no ponto \(1\).
A)\(\frac{19}{26}\),
B)\(\frac{8}{13}\),
C)\(\frac{7}{26}\),
D)\(\frac{5}{13}\)
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt