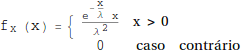Estimativa de máxima verosimilhança - distribuição gama
Saltar para a navegação
Saltar para a pesquisa
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Probabilidades e Estatística
- ANO: 2
- LINGUA: pt
- AUTOR: Equipa de Probabilidades e Estatística
- MATERIA PRINCIPAL: Amostragem e estimação pontual
- DESCRICAO: Estimativa de máxima verosimilhança - distribuição gama
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 10 min
- TEMPO MAXIMO DE RESOLUCAO: 15 min
- PALAVRAS CHAVE: função de verosimilhança, estimativa de máxima verosimilhança, distribuição gama
Admita que os tempos (em centena de hora) entre avarias consecutivas de um sistema são variáveis aleatórias independentes e identicamente distribuídas à variável aleatória \(X\) com função de densidade de probabilidade dada por
onde \( \lambda \) é um parâmetro desconhecido positivo. A concretização de uma amostra aleatória de dimensão \(50\) de \(X\) conduziu a \(\pmb{\sum_{i=1}^{50}x_i}\)=\(518.45\). Obtenha a estimativa de máxima verosimilhança de \( \lambda \). Preencha a caixa abaixo com o resultado obtido com, pelo menos, três casas decimais.
Para obter o zip que contém as instâncias deste exercício clique aqui[1]
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt