Diferenças entre edições de "Esfera eletrizada rodeada por coroas esféricas"
Saltar para a navegação
Saltar para a pesquisa
(Criou a página com "<div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> '''Metadata''' <div class="mw-collapsible-content"> *CONTEXTO : Primeiro ciclo universitário *AREA...") |
|||
| Linha 9: | Linha 9: | ||
*AUTOR: Jorge Loureiro | *AUTOR: Jorge Loureiro | ||
*MATERIA PRINCIPAL: Eletrostática na matéria | *MATERIA PRINCIPAL: Eletrostática na matéria | ||
| − | *DESCRICAO: Determinação do | + | *DESCRICAO: Determinação do campo e do potencial elétricos no espaço. Determinação da carga elétrica de polarização e da pressão eletrostática. |
*DIFICULDADE: **** | *DIFICULDADE: **** | ||
*TEMPO MEDIO DE RESOLUCAO: 15 min | *TEMPO MEDIO DE RESOLUCAO: 15 min | ||
*TEMPO MAXIMO DE RESOLUCAO: 30 min | *TEMPO MAXIMO DE RESOLUCAO: 30 min | ||
| − | *PALAVRAS CHAVE: campo elétrico, condensador, dielétrico, potencial, Poisson | + | *PALAVRAS CHAVE: campo elétrico, condensador, dielétrico, potencial, Poisson, esfera |
</div> | </div> | ||
</div> | </div> | ||
Edição atual desde as 16h36min de 1 de outubro de 2015
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Física
- DISCIPLINA: Eletromagnetismo e Óptica
- ANO: 2
- LINGUA: pt
- AUTOR: Jorge Loureiro
- MATERIA PRINCIPAL: Eletrostática na matéria
- DESCRICAO: Determinação do campo e do potencial elétricos no espaço. Determinação da carga elétrica de polarização e da pressão eletrostática.
- DIFICULDADE: ****
- TEMPO MEDIO DE RESOLUCAO: 15 min
- TEMPO MAXIMO DE RESOLUCAO: 30 min
- PALAVRAS CHAVE: campo elétrico, condensador, dielétrico, potencial, Poisson, esfera
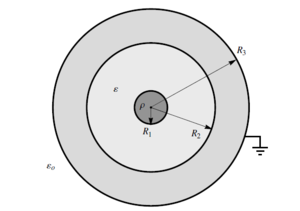
Uma esfera de raio \(R_1\) uniformemente eletrizada em volume com uma carga de densidade \( \rho \), encontra-se rodeada por uma coroa esférica dielétrica, de raios \(R_1\) e \(R_2\) e permitividade \( \epsilon \) constante, e por uma coroa esférica condutora de raios \(R_2\) e \(R_3\) (ver figura).
- Supondo que a coroa esférica está ligada à terra, determine o campo eletrostático em todos os pontos do espaço e as densidades de carga elétrica nas superfícies da coroa esférica condutora.
- Determine o potencial elétrico em todos os pontos do espaço.
- Determine as densidades de carga elétrica de polarização e a pressão eletrostática que atua sobre a superfície interior da coroa esférica condutora.