Diferenças entre edições de "Conjuntos em \(R^2\)"
| Linha 9: | Linha 9: | ||
*AUTOR: Equipa Calculo diferencial e integral 2 | *AUTOR: Equipa Calculo diferencial e integral 2 | ||
*MATERIA PRINCIPAL: Estrutura algébrica e topológica de \(R^n\) | *MATERIA PRINCIPAL: Estrutura algébrica e topológica de \(R^n\) | ||
| − | *DESCRICAO: | + | *DESCRICAO: conjuntos em \(R^2\) |
*DIFICULDADE: easy | *DIFICULDADE: easy | ||
*TEMPO MEDIO DE RESOLUCAO: 15 mn | *TEMPO MEDIO DE RESOLUCAO: 15 mn | ||
*TEMPO MAXIMO DE RESOLUCAO: 30 mn | *TEMPO MAXIMO DE RESOLUCAO: 30 mn | ||
| − | *PALAVRAS CHAVE: | + | *PALAVRAS CHAVE: conjunto limitado, conjunto fechado, interior, exterior, fronteira, |
</div> | </div> | ||
</div> | </div> | ||
Revisão das 19h18min de 20 de março de 2018
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo diferencial e integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Equipa Calculo diferencial e integral 2
- MATERIA PRINCIPAL: Estrutura algébrica e topológica de \(R^n\)
- DESCRICAO: conjuntos em \(R^2\)
- DIFICULDADE: easy
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 30 mn
- PALAVRAS CHAVE: conjunto limitado, conjunto fechado, interior, exterior, fronteira,
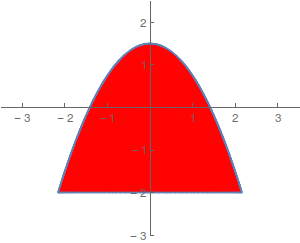
Seja \(\text{A$\subset$}\mathbb{R}^2\) um conjunto limitado e fechado do plano com a seguinte representação geométrica:
Seleccione todas as afirmações correctas.
A)O conjunto fronteira de A pode ser dado por \(\left\{\left(\begin{array}{c}x\\y\\\end{array}\right)\text{$\in$}\mathbb{R}^2\text{:}\left(3x^2+4y=6\land y\geq-2\right)\lor\left(y=-2\land3x^2+4y\leq6\right)\right\}\).
B)O conjunto A pode ser dado por \(\left\{\left(\begin{array}{c}x\\y\\\end{array}\right)\text{$\in$}\mathbb{R}^2\text{:}3x^2+4y>6\land y\leq-2\right\}\).
C)O conjunto interior de A pode ser dado por \(\left\{\left(\begin{array}{c}x\\y\\\end{array}\right)\text{$\in$}\mathbb{R}^2\text{:}3x^2+4y<6\land y>-2\right\}\).
D)Nenhuma das anteriores
Para obter o zip que contém as instâncias deste exercício clique aqui(conjuntos2D)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt