Comprimento de curva paramétrica
Metadata
- CONTEXTO : Primeiro ciclo universitário
- AREA: Matemática
- DISCIPLINA: Calculo Diferencial e Integral 2
- ANO: 1
- LINGUA: pt
- AUTOR: Ana Moura Santos e Miguel Dziergwa
- MATERIA PRINCIPAL: Integrais de linha: integrais de campos escalares e campos vetoriais
- DESCRICAO: Comprimento de curva paramétrica
- DIFICULDADE: **
- TEMPO MEDIO DE RESOLUCAO: 15 mn
- TEMPO MAXIMO DE RESOLUCAO: 20 mn
- PALAVRAS CHAVE: integral de linha, comprimento de curva paramétrica
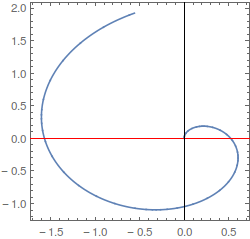
Na figura seguinte pode ver-se a representação geométrica da curva parametrizada por \( \gamma (t)=\)\(\left(\begin{array}{c}t\sin(3t)\\t\cos(3t)\\\end{array}\right)\) com \(t \in [ \)\(0\),\(2\)\( ] \).
Qual das seguintes expressões pode corresponder ao comprimento de arco da curva nesse intervalo?
A) \(\sqrt{37}+\frac{1}{6}\log\left(6+\sqrt{37}\right)\)
B) \(\sqrt{\frac{5}{2}}+3\sqrt{\frac{41}{2}}+\frac{1}{6}\log\left(3+\sqrt{10}\right)+\frac{1}{6}\log\left(9+\sqrt{82}\right)\)
C) \(\sqrt{37}-1\)
D) \(-2\sqrt{37}-\frac{1}{3}\log\left(6+\sqrt{37}\right)\)
Para obter o zip que contém as instâncias deste exercício clique aqui(paramComprimento)
Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt