Combinação de áreas

Metadata

• CONTEXTO : Primeiro ciclo universitário
• AREA: Matemática
• DISCIPLINA: Calculo diferencial e integral 1
• ANO: 1
• LINGUA: pt
• AUTOR: Ana Moura Santos e Miguel Dziergwa
• MATERIA PRINCIPAL:
• DESCRICAO:
• DIFICULDADE: *
• TEMPO MEDIO DE RESOLUCAO: 10 mn
• TEMPO MAXIMO DE RESOLUCAO: 15 mn
• PALAVRAS CHAVE:

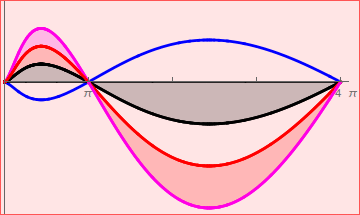
Na figura abaixo estão representados os gráficos das funções \( f(x), -a.f(x), b.f(x) \) e \( c.f(x) \), com \(1<a<b<c\), definidas no intervalo \( [0,4 \pi ] \) e com um zero no ponto \( x= \pi \).

A área sombreada é dada por:

A) \((b-c-1)\int_{\pi}^{4\pi}f(x)\,dx+c\int_0^{\pi}f(x)\,dx\),

B) \((b-1)\int_0^{\pi}f(x)\,dx-c\int_{\pi}^{4\pi}f(x)\,dx\),

C) \((a+1)\int_0^{\pi}f(x)\,dx-(a-b+c+1)\int_{\pi}^{4\pi}f(x)\,dx\),

D) \((-b+c-1)\int_{\pi}^{4\pi}f(x)\,dx+b\int_0^{\pi}f(x)\,dx\)

Para obter o zip que contém as instâncias deste exercício clique aqui(combinacaoAreas)

Se deseja obter o código fonte que gera os exercícios contacte miguel.dziergwa@ist.utl.pt